buk_notes/00.md

Größenvergleiche zwischen Mengen

• A \geq B \iff \exists f : A \to B \text{ mit } f \text{ surjektiv }
• A \leq B \iff \exists f : A \to B \text{ mit } f \text{ injektiv }
• A = B \iff \exists f : A \to B \text{ mit } f \text{ bijektiv }

Cantors Diagonalargument

\mathcal P(\mathbb N) ist überabzählbar, also | \mathcal P(\mathbb N) | = | \mathbb R |

Berechenbarkeit

• Undefiniert (meist: hält nicht) = gibt keinen wert: \perp
• Nicht Berechenbar = gibt einen Wert aber keinen weg dorthin, wir wissen halt z.B. dass x \in B
• Partiell = mind. 1 eingabe undefiniert
• Nicht Berechenbar = mind. für 1 Eingabe ist die Ausgabe nicht berechenbar

Turingmaschine

Gerne zeiger auf startposition zurückstellen

Turing-Berechenbar \implies Berechenbar

Nach Church-Turing-These: Berechenbar \implies Turing-Berechenbar

TM-Definition immer aufschreiben: Septupel (\text{Zustandsmenge}, \text{Eingabealphabet}, \text{Arbeitsalphabet}, \delta \text{funktion}, z_0, \square, \text{Akzeptierende Zustände})

• die ersten 4 sind müde (EEEP) → 3× endlich, 4. ist partiell.
• z_0 \in \text{Akzeptierende Zustände} ist valide, Akzeptieren \neq Halten
• Anfangszustand des Bands besteht aus Eingabealphabet und Blanks, Band kann dann von TM auf ganzes Arbeitsalphabet erweitert werden
• Turing-Maschine hält gdw. \delta(\dots) = \perp , also Undefiniert
• Ausgabe steht meist auf Band, bool können aber auch als "liegt letzter zustand in Akzeptierenden Zuständen?" dargestellt werden
• \delta : (\text{Zustandsmenge}, \text{Arbeitsalphabet}) \to (\text{Arbeitsalphabet}, \{ L, N, R \}, \text{Zustandsmenge}) (Reihenfolge may be different, me didnt verify | TODO)

Konfiguration

• Alphabets-Elemente links vom Zeiger + Aktueller Zustand + Elemente am und rechts vom Zeiger
  • bzw: Alphabets-Elemente links vom Zeiger + Aktueller Zustand + Zeigersymbol + Elemente rechts vom Zeiger
  • ignoriere blanks links/rechts vom "letzten" non-blank

Gleichmächtige TMs

• Zweiband mit 1 oder 2 Zeiger(n)
• Nur Einseitig Unendlich
• Always-Moving (nur L und R, kein N)
• TM auf Eingabealphabet \{ 0, 1 \}

Berechnungsmodelle

Primitiv-Rekursiv = LOOP < GOTO = WHILE = TM = µ-Rekursiv

LOOP

Syntax:

• x_i := x_j \{+,-\} c (NOTE: x_i := x_j + 0, NOTE 2: 4-6=0 , d.h. saturating subtraction bei LOOP, WHILE, und GOTO)
• P_1 ; P_2
• \text{LOOP } x_i \text{ DO } P \text{ END}
• es gibt erstmal kein \text{IF}

jedes LOOP-programm berechnet eine totale funktion, d.h. es gibt kein \perp (LOOP \implies total)

Konventionen:

• Variablen sind by default 0
• Eingaben sind x_1, x_2, \dots
• Ausgabe ist x_0

Primitiv Rekursiv

Definition:

• Nullfunktion null = null(x) = null(x, y) = \dots = 0
• Nachfolgerfunktion succ(n) = n + 1
• Projektionen id(n) = n, id_1(n,m) = n, id_2(n,m) = m, \dots
• Kompositionen f(a, g(b)) (ohne rekursion)
  • PR-Aufgebaute Funktionen f(a, b, c) = g(i(a), j(b))
• Rekursive Aufrufe sind möglich, z.B.: r(a, b, c) = r(a-1, b, c) (für a > 0 )
  • Dabei gibt es einen Basisfall r(0, b, c) = g(b, c) für a = 0
  • und einen Rekursionsfall r(a+1,b,c) = h(r(a, b, c), a, b, c) ,
  • wobei man nur g und h selbst wählen kann, nicht deren Argumente (die sind gegeben wie oben, man kriegt nur den rekursiven Wert für r(a-1,b,c) in h und sonst keinen! Aber Eingaben dürfen weggelassen werden)
  • wobei g und h Primitiv Rekursiv sein müssen
  • Wir schreiben beim Rekursionsfall (damit man es nicht so leicht falsch machen kann) r(a+1, b, c) = \dots , wobei nur ein +1 , und auch nur +1 , erlaubt ist
  • Beispiel: add(0, x) = x, \quad add(y+1, x) = succ(add(y,x)) ist als PR: g(x) \; : \; g = id, \quad h(add(y,x), y, x) \; : \; h = succ \circ id_1

ES IST SO SKUFFED, MACH IMMER! EIN LOOP PROGRAMM

µ-Rekursiv

Definition wie die der Primitiv Rekursiven Funktionen, aber zusätzlich der \mu Operator:

\mu f (a, b, c) = \min \{ n \vert f(n, a, b, c) = 0 \text{ und } f(m, a, b, c) \text{ definiert für alle } m < n \} ,
d.h. probier alle n \in \mathbb N_0 in aufsteigender Reihenfolge bis f(n, \dots) = 0 , dann return n , sonst keep searching.
If f(n, \dots) \neq 0 oder f(n, \dots) vor einer 0 undefiniert ( \perp ), dann ist \mu f (\dots) undefiniert, also \perp

WHILE / GOTO

WHILE ist wie LOOP, aber statt LOOP mit \text{WHILE } x_i \neq 0 \text{ DO } P \text{ END} .

GOTO ist wie LOOP, aber statt LOOP mit Sprüngen \text{GOTO } M_i und \text{IF } x_i = c \text{ THEN GOTO } M_i , und der Stopanweisung \text{HALT} .

Man kann jedes WHILE-Programm mit in eines mit nur einem WHILE-Loop umschreiben,
und jedes GOTO-Programm in eines mit nur einem Rücksprung umschreiben.

µ-Rekursive (= WHILE/GOTO) Funktionen sind nicht immer total, können aber total sein.

Universelle TM

Es existieren Universelle TMs, Universelle WHILE- und GOTO-Programme, die jegliches WHILE-/GOTO-Programm ausführen können.

Das geht mit nur Primitiver Rekursion (z.B. LOOP) nicht!

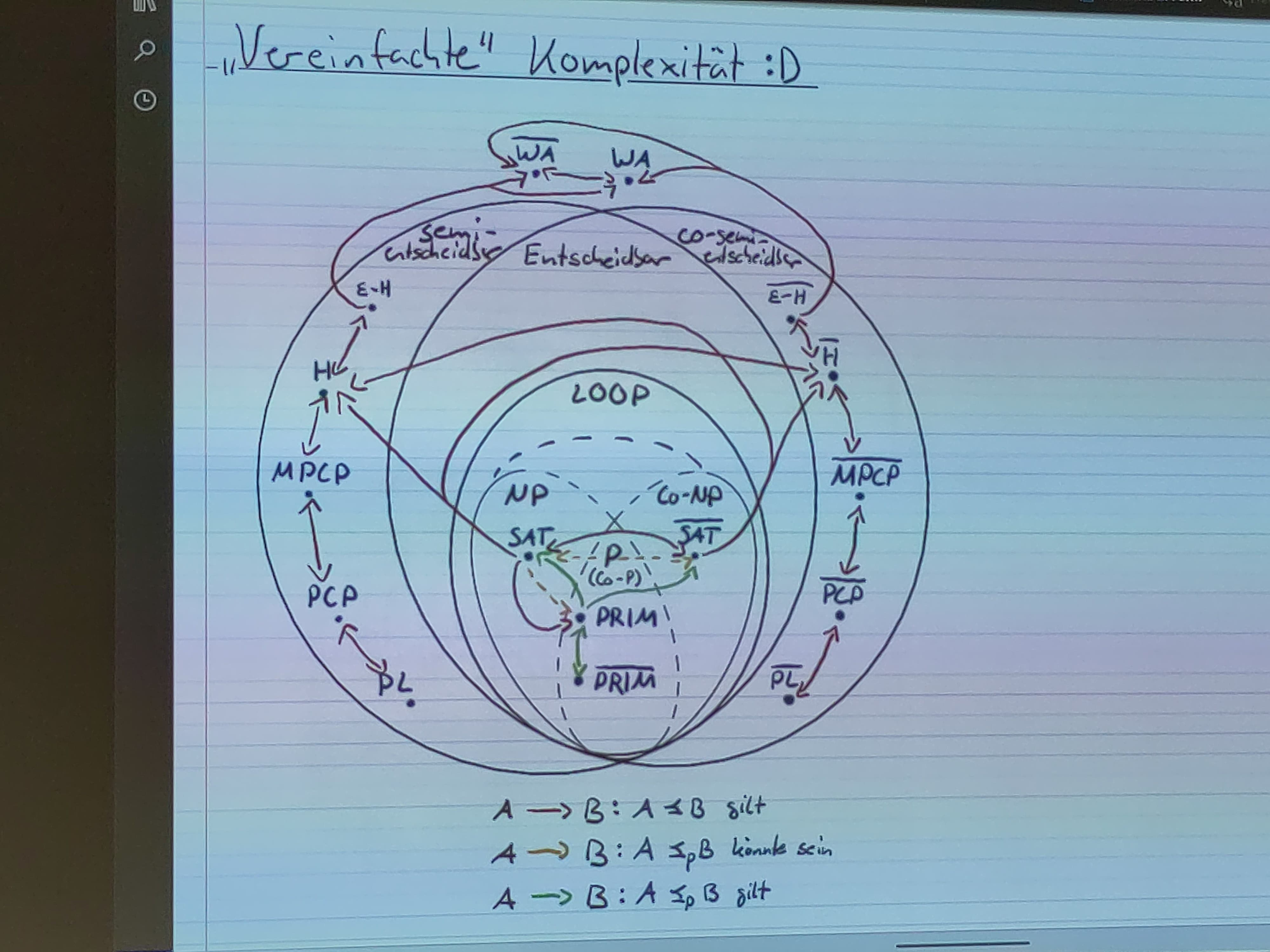
Entscheidungsprobleme

\exists A, \overline A \subseteq U und x \in U . Frage: x \in A ? (Wenn nicht, dann x \in \overline A ).

• Ist n \in \mathbb N gerade? ( \text{EVEN} \subseteq \mathbb N )
• Ist die aussagenlogische Formel F erfüllbar? ( \text{SAT} \subseteq Menge aller aussagenlogischen Formeln)
• Halteproblem H : Hält die TM auf der Eingabe x ? ( H \subseteq Menge aller TMs und ihrer Eingaben)
  • Halteproblem auf dem leeren Band H_0 , wie oben nur mit x = leeres Band (ist auch nur semi-entscheidbar)

Entscheidbarkeit

Problem P ist entscheidbar \iff die Charakteristische Funktion f existiert und ist berechenbar, mit f = \begin{cases} 1, & x \in A, 0, & x \in \overline A \end{cases}

Entscheidbar \iff Semi-Entscheidbar ( x \in A \to 1, x \in \overline A \to 0 oder \perp ) und Co-Semi-Entscheidbar ( x \in \overline A \to 0, x \in A \to 1 oder \perp )

→ H ist nur Semi-Entscheidbar, nicht Entscheidbar.

Gleiches gilt laut Satz von Rice für jegliche nichttriviale Eigenschaft von Algorithmen (TMs), also jedes Entscheidungsproblem
\emptyset \subset A \subset \text{Alle möglichen Turingmaschinen}
ist unentscheidbar (kann aber semi-entscheidbar sein). (bezogen auf Algorithmen, ohne inputs)

Rekursiv Aufzählbar

A ist rekursiv aufzählbar, wenn eine totale, berechenbare, surjektive (ganz A abgedeckt) Funktion f : \mathbb N \to A existiert.

Arithmetische Aussagen

WA = Wahre Arithmetische Aussagen

WA ist Unentscheidbar, und auch weder semi- noch co-semi-entscheidbar, da WA Überabzählbar Unendlich ist.

Reduktion \preceq

Seien A, B \subseteq U zwei Entscheidungsprobleme.

Es ist A auf B reduzierbar, d.h. A \preceq B , falls es eine Reduktion gibt:

Eine Reduktion ist eine totale, berechenbare Funktion f : U \to U , sodass x \in A \iff f(x) \in B

Falls A \preceq B und B entscheidbar (bzw. (co-)semi-entscheidbar), dann gilt das auch für A .

\to Wir reduzieren A auf B , A \preceq B , und nehmen dann (mind.) die Entscheidbarkeit von B auch für A an.

Dabei gilt:

• A entscheidbar \iff A semi- und co-semi-entscheidbar
• A semi-entscheidbar \iff \overline A co-semi-entscheidbar
• aus A \preceq B folgt:
  • A entscheidbar \Leftarrow B entscheidbar
    • und das gleiche mit (co-)semi-entscheidbar
  • A unentscheidbar \implies B unentscheidbar
    • und das gleiche mit (co-)semi-entscheidbar
• A \preceq B \land B \preceq C \implies A \preceq C

PCP und MPCP

Not really gonna explain what PCP is.
We add top to left string, bottom to right string, want them to be equal.
MPCP requires that we start with the first pair.

PCP ist nur semi-entscheidbar.

Beispiel: \begin{pmatrix} \text{aa} \\ \text{b} \end{pmatrix}, \begin{pmatrix} \text{b} \\ \text{bb} \end{pmatrix}, \begin{pmatrix} \text{ba} \\ \text{a} \end{pmatrix}, \begin{pmatrix} \text{b} \\ \text{aa} \end{pmatrix}

Mögliche Lösungen: 23, 2413, 2323, 232413, \dots

P und NP

P (Polynomiell) ist die Menge der in Polynomieller Zeit von einer (deterministischen) Turing-Maschine entscheidbaren Probleme.

NP ist die Menge der in Polynomieller Zeit von einer nicht-deterministischen Turing-Maschine entscheidbaren Probleme.

Es gilt P \subseteq NP, P = NP ist nicht gezeigt <insert n=1 \lor p=0 joke here>

NP-Hart: Mind. so schwer wie alle Probleme in NP
NP-Vollständig: Ein Problem ist NP-Vollständig, wenn es NP-Hart ist und in NP liegt

+———————————————————+
|         +—————+   |
|   NP    |  P  |   |
|         +—————+   |
|                   |
|  +————————————————+—————————+
|  | NP-Vollständig |         |
+——+————————————————+ NP-Hart |
   |                          |
   +——————————————————————————+

• SAT ist NP-Vollständig

Polyzeit-Reduktion ( \preceq_p )

Eine Polyzeit-Reduktion ist eine Reduktion, die in polynomieller Zeit berechnet werden kann.
(Polyzeit-Reduktion ist für Aufwand/Laufzeit, normale Reduktion ist für Entscheidbarkeit)

• Wenn A \preceq_p B und B \in \text{NP}, dann liegt A auch in \text{NP}
• Wenn C \preceq_p A und C NP-Hart, dann ist A NP-Hart

Credits an Matthias