buk_notes/00.md

Größenvergleiche zwischen Mengen

• A \geq B \iff \exists f : A \to B \text{ mit } f \text{ surjektiv }
• A \leq B \iff \exists f : A \to B \text{ mit } f \text{ injektiv }
• A = B \iff \exists f : A \to B \text{ mit } f \text{ bijektiv }

Cantors Diagonalargument

\mathcal P(\mathbb N) ist überabzählbar, also | \mathcal P(\mathbb N) | = | \mathbb R |

Berechenbarkeit

• Undefiniert (meist: hält nicht) = gibt keinen wert: \perp
• Nicht Berechenbar = gibt einen Wert aber keinen weg dorthin, wir wissen halt z.B. dass x \in B
• Partiell = mind. 1 eingabe undefiniert
• Nicht Berechenbar = mind. für 1 Eingabe ist die Ausgabe nicht berechenbar

Turingmaschine

Gerne zeiger auf startposition zurückstellen

Turing-Berechenbar \implies Berechenbar

Nach Church-Turing-These: Berechenbar \implies Turing-Berechenbar

TM-Definition immer aufschreiben: Septupel (\text{Zustandsmenge}, \text{Eingabealphabet}, \text{Arbeitsalphabet}, \delta \text{funktion}, z_0, \square, \text{Akzeptierende Zustände})

• die ersten 4 sind müde (EEEP) → 3× endlich, 4. ist partiell.
• z_0 \in \text{Akzeptierende Zustände} ist valide, Akzeptieren \neq Halten
• Anfangszustand des Bands besteht aus Eingabealphabet und Blanks, kann von TM auf ganzes Arbeitsalphabet erweitert werden
• Turing-Maschine hält gdw. \delta(\dots) = \perp , also Undefiniert
• Ausgabe steht meist auf Band, bool können aber auch als "liegt letzter zustand in Akzeptierenden Zuständen?" dargestellt werden
• \delta : (\text{Zustandsmenge}, \text{Arbeitsalphabet}) \to (\text{Arbeitsalphabet}, \{ L, N, R \}, \text{Zustandsmenge}) (Reihenfolge may be different, me didnt verify | TODO)

Konfiguration

• Alphabets-Elemente links vom Zeiger + Aktueller Zustand + Elemente am und rechts vom Zeiger
  • bzw: Alphabets-Elemente links vom Zeiger + Aktueller Zustand + Zeigersymbol + Elemente rechts vom Zeiger
  • ignoriere blanks links/rechts vom "letzten" non-blank

Gleichmächtige TMs

• Zweiband mit 1 oder 2 Zeiger(n)
• Nur Einseitig Unendlich
• Always-Moving (nur L und R, kein N)
• TM auf Eingabealphabet \{ 0, 1 \}

Berechnungsmodelle

Primitiv-Rekursiv = LOOP < GOTO = WHILE = TM = µ-Rekursiv

LOOP

Syntax:

• x_i := x_j \{+,-\} c (NOTE: x_i := x_j + 0 4-6=0 , d.h. saturating subtraction bei LOOP, WHILE, und GOTO)
• P_1 ; P_2
• \text{LOOP } x_i \text{ DO } P \text{ END}
• no \text{IF}

jedes LOOP-programm berechnet eine totale funktion, d.h. es gibt kein \perp (LOOP \implies total)

Konventionen:

• Variablen sind by default 0
• Eingaben sind x_1, x_2, \dots
• Ausgabe ist x_0

Primitiv Rekursiv

Definition:

• Nullfunktion null = null(x) = null(x, y) = \dots = 0
• Nachfolgerfunktion succ(n) = n + 1
• Projektionen id(n) = n, id_1(n,m) = n, id_2(n,m) = m, \dots
• Kompositionen f(a, g(b)) (ohne rekursion)
  • PR-Aufgebaute Funktionen f(a, b, c) = g(i(a), j(b))
• Rekursive Aufrufe sind möglich, z.B.: r(a, b, c) = r(a-1, b, c) (für a > 0 )
  • Dabei gibt es einen Basisfall r(0, b, c) = g(b, c) für a = 0
  • und einen Rekursionsfall r(a+1,b,c) = h(r(a, b, c), a, b, c) ,
  • wobei man nur g und h selbst wählen kann, nicht deren Argumente (die sind gegeben wie oben, man kriegt nur den rekursiven Wert für r(a-1,b,c) in h und sonst keinen! Aber Eingaben dürfen weggelassen werden)
  • wobei g und h Primitiv Rekursiv sein müssen
  • Wir schreiben beim Rekursionsfall (damit man es nicht so leicht falsch machen kann) r(a+1, b, c) , wobei nur ein +1 , und auch nur +1 , erlaubt ist
  • Beispiel: add(0, x) = x, \quad add(y+1, x) = succ(add(y,x)) ist als PR: g(x) \; : \; g = id, \quad h(add(y,x), y, x) \; : \; h = succ \circ id_1

ES IST SO SKUFFED, MACH IMMER! EIN LOOP PROGRAMM

µ-Rekursiv

Zusatz zur Definition der Primitiv Rekursiven Funktionen:

\mu f (a, b, c) = \min \{ n \vert f(n, a, b, c) = 0 \text{ und } f(m, a, b, c) \text{ definiert für alle } m < n \} ,
d.h. probier alle n \in \mathbb N_0 in aufsteigender Reihenfolge bis f(n, \dots) = 0 , dann return n , sonst keep searching. If f(n, \dots) \neq 0 , dann ist \mu f (\dots) undefiniert, also \perp

WHILE / GOTO

WHILE ist wie LOOP, aber statt LOOP mit \text{WHILE } x_i \neq 0 \text{ DO } P \text{ END} .

GOTO ist wie LOOP, aber statt LOOP mit Sprüngen \text{GOTO } M_i und \text{IF } x_i = c \text{ THEN GOTO } M_i , und der Stopanweisung \text{HALT} .

Man kann jedes WHILE-Programm mit in eines mit nur einem WHILE-Loop umschreiben,
und jedes GOTO-Programm in eines mit nur einem Rücksprung umschreiben.

µ-Rekursive (= WHILE/GOTO) Funktionen sind nicht immer total, können aber total sein.

Universelle TM

Es existieren Universelle TMs, Universelle WHILE- und GOTO-Programme, die jegliches WHILE-/GOTO-Programm ausführen können.

Das geht mit nur Primitiver Rekursion (z.B. LOOP) nicht!

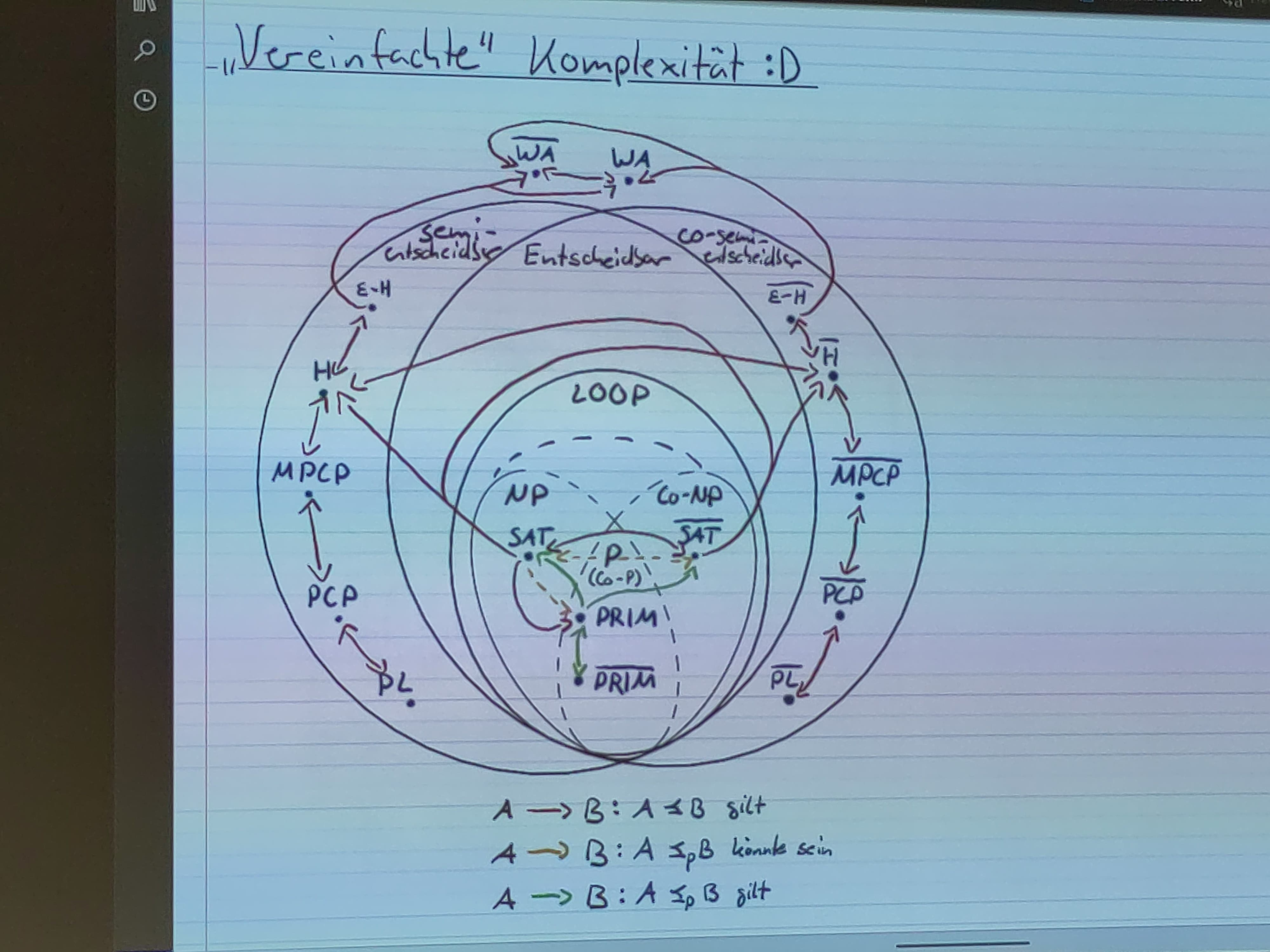
Entscheidungsprobleme

\exists A, \overline A \subseteq U und x \in U . Frage: x \in A ? (Wenn nicht, dann x \in \overline A ).

• Ist n \in \mathbb N gerade? ( \text{EVEN} \subseteq \mathbb N )
• Ist die aussagenlogische Formel F erfüllbar? ( \text{SAT} \subseteq Menge aller aussagenlogischen Formeln)
• Halteproblem H : Hält die TM auf der Eingabe x ? ( H \subseteq Menge aller TMs und ihrer Eingaben)
  • Halteproblem auf dem leeren Band H_0 , wie oben nur mit x = leeres Band (ist auch nur semi-entscheidbar)

Entscheidbarkeit

Problem P ist entscheidbar \iff die Charakteristische Funktion f existiert und ist berechenbar, mit f = \begin{cases} 1, & x \in A, 0, & x \in \overline A \end{cases}

Entscheidbar \iff Semi-Entscheidbar ( x \in A \to 1, x \in \overline A \to 0 oder \perp ) und Co-Semi-Entscheidbar ( x \in \overline A \to 0, x \in A \to 1 oder \perp )

→ H ist nur Semi-Entscheidbar, nicht Entscheidbar.

Gleiches gilt laut Satz von Rice für jegliche nichttriviale Eigenschaft von Algorithmen (TMs), also jedes Entscheidungsproblem \emptyset \subset A \subset \text{Alle möglichen Turingmaschinen} ist unentscheidbar (kann aber semi-entscheidbar sein). (bezogen auf Algorithmen, ohne inputs)

Rekursiv Aufzählbar

A ist rekursiv aufzählbar, wenn eine totale, berechenbare, surjektive (ganz A abgedeckt) Funktion f : \mathbb N \to A

Arithmetische Aussagen

WA = Wahre Arithmetische Aussagen

WA ist Unentscheidbar, und auch weder semi- noch co-semi-entscheidbar, da WA Überabzählbar Unendlich ist.

Reduktion \preceq

Seien A, B \subseteq U zwei Entscheidungsprobleme.

Es ist A auf B reduzierbar, d.h. A \preceq B , falls es eine Reduktion gibt:

Eine Reduktion ist eine totale, berechenbare Funktion f : U \to U , sodass x \in A \iff f(x) \in B

Falls A \preceq B und B entscheidbar (bzw. (co-)semi-entscheidbar), dann gilt das auch für A .

\to Wir reduzieren A auf B , A \preceq B , und nehmen dann (mind.) die Entscheidbarkeit von B auch für A an.

Dabei gilt:

• A entscheidbar \iff A semi- und co-semi-entscheidbar
• A semi-entscheidbar \iff \overline A co-semi-entscheidbar
• aus A \preceq B folgt:
  • A entscheidbar \Leftarrow B entscheidbar
    • und das gleiche mit (co-)semi-entscheidbar
  • A unentscheidbar \implies B unentscheidbar
    • und das gleiche mit (co-)semi-entscheidbar
• A \preceq B \land B \preceq C \implies A \preceq C

PCP und MPCP

Not really gonna explain what PCP is. We add top to left string, bottom to right string, want them to be equal.

PCP ist nur semi-entscheidbar.

Beispiel: \begin{pmatrix} \text{aa} \\ \text{b} \end{pmatrix}, \begin{pmatrix} \text{b} \\ \text{bb} \end{pmatrix}, \begin{pmatrix} \text{ba} \\ \text{a} \end{pmatrix}, \begin{pmatrix} \text{b} \\ \text{aa} \end{pmatrix}

Mögliche Lösungen: 23, 2413, 2323, 232413, \dots

P und NP

P (Polynomiell) ist die Menge der in Polynomieller Zeit von einer (deterministischen) Turing-Maschine entscheidbaren Probleme.

NP ist die Menge der in Polynomieller Zeit von einer nicht-deterministischen Turing-Maschine entscheidbaren Probleme.

Es gilt P \subseteq NP, P = NP ist nicht gezeigt <insert n=1 \lor p=0 joke here>

NP-Hart: Mind. so schwer wie alle Probleme in NP
NP-Vollständig: Ein Problem ist NP-Vollständig, wenn es NP-Hart ist und in NP liegt

+———————————————————+
|         +—————+   |
|   NP    |  P  |   |
|         +—————+   |
|                   |
|  +————————————————+—————————+
|  | NP-Vollständig |         |
+——+————————————————+ NP-Hart |
  .|                          |
  .+——————————————————————————+

• SAT ist NP-Vollständig

Polyzeit-Reduktion ( \preceq_p )

Eine Polyzeit-Reduktion ist eine Reduktion, die in polynomieller Zeit berechnet werden kann.
(Polyzeit-Reduktion ist für Aufwand/Laufzeit, normale Reduktion ist für Entscheidbarkeit)

• Wenn A \preceq_p B und B \in \text{NP}, dann liegt A auch in \text{NP}
• Wenn C \preceq_p A und C NP-Hart, dann ist A NP-Hart

Credits an Matthias